基于用户的协同过滤
我们将一个用户和其他所有用户进行对比,找到相似的人。这种算法有两个弊端:
扩展性 随着用户数量的增加,其计算量也会增加。这种算法在只有几千个用户的情况下能够工作得很好,但达到一百万个用户时就会出现瓶颈。
稀疏性 大多数推荐系统中,物品的数量要远大于用户的数量,因此用户仅仅对一小部分物品进行了评价,这就造成了数据的稀疏性。比如亚马逊有上百万本书,但用户只评论了很少一部分,于是就很难找到两个相似的用户了。
鉴于以上两个局限性,我们不妨考察一下基于物品的协同过滤算法。
基于物品的协同过滤
假设我们有一种算法可以计算出两件物品之间的相似度,比如Phoenix专辑和Manners很相似。如果一个用户给Phoenix打了很高的分数,我们就可以向他推荐Manners了。
需要注意这两种算法的区别:
修正的余弦相似度
我们使用余弦相似度来计算两个物品的距离。上一章提过“分数膨胀”现象,因此我们会从用户的评价中减去他所有评价的均值,这就是修正的余弦相似度。
 = \frac{\sum_{u\in U}(R_{u,i} - \overline R_{u})(R_{u,j} - \overline R_{u})} {\sqrt{\sum_{u\in U}(R_{u,i} - \overline R_{u})^2}\sqrt{\sum_{u\in U}(R_{u,j} - \overline R_{u})^2}})
U表示同时评价过物品i和j的用户集合。
计算修正余弦相似度的Python代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| # -*- coding: utf-8 -*-
from math import sqrt
users3 = {"David": {"Imagine Dragons": 3, "Daft Punk": 5,
"Lorde": 4, "Fall Out Boy": 1},
"Matt": {"Imagine Dragons": 3, "Daft Punk": 4,
"Lorde": 4, "Fall Out Boy": 1},
"Ben": {"Kacey Musgraves": 4, "Imagine Dragons": 3,
"Lorde": 3, "Fall Out Boy": 1},
"Chris": {"Kacey Musgraves": 4, "Imagine Dragons": 4,
"Daft Punk": 4, "Lorde": 3, "Fall Out Boy": 1},
"Tori": {"Kacey Musgraves": 5, "Imagine Dragons": 4,
"Daft Punk": 5, "Fall Out Boy": 3}}
def computeSimilarity(band1, band2, userRatings):
"""
:param band1:物品1
:param band2:物品2
:param userRatings:用户评分dict
averages = {}
for (key, ratings) in userRatings.items():
averages[key] = float(sum(ratings.values()))/len(ratings.values())
num = 0 # 分子
dem1 = 0 # 分母的第一部分
dem2 = 0 #
for (user, ratings) in userRatings.items():
if band1 in ratings and band2 in ratings:
avg = averages[user]
num += (ratings[band1] - avg) * (ratings[band2] - avg)
dem1 += (ratings[band1] - avg)**2
dem2 += (ratings[band2] - avg)**2
return num / (sqrt(dem1) * sqrt(dem2))
print computeSimilarity('Kacey Musgraves', 'Lorde', users3)
print computeSimilarity('Imagine Dragons', 'Lorde', users3)
print computeSimilarity('Daft Punk', 'Lorde', users3)
Output:
0.320959291341
-0.252526537229
0.784114958467
|
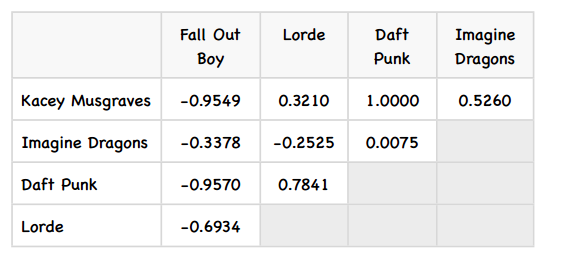
相似度矩阵的预测
这个矩阵看起来不错,那下面该如何使用它来做预测呢?比如我想知道David有多喜欢Kecey Musgraves?
 = \frac{\sum_{N\in similarTo(i)}(S_{i,N}\times R_{u,N})}{\sum_{N\in similarTo(i)}(|S_{i,N}|)})
p(u,i)表示我们会来预测用户u对物品i的评分,所以p(David, Kacey Musgraves)就表示我们将预测David会给Kacey打多少分。
N是一个物品的集合,有如下特性:用户u对集合中的物品打过分;物品i和集合中的物品有相似度数据(即上文中的矩阵)。
 表示物品i和N的相似度,
表示物品i和N的相似度,  表示用户u对物品N的评分。
表示用户u对物品N的评分。
归一化转换
为了让公式的计算效果更佳,对物品的评价分值最好介于-1和1之间。由于我们的评分系统是1至5星,所以需要使用一些运算将其转换到-1至1之间。
 - (Max_{R} - Min_{R}) }{(Max_{R} - Min_{R})})
比如一位用户给Fall Out Boy打了2分,那修正后的评分为:
$$ NR_{u,N} = \frac{2(2-1) - (5-1)}{5-1} = -2/4 = -0.5 $$
反过来则是:
\times(Max_{R} - Min_{R})) + Min_{R} = \frac12((-0.5 + 1)*4) + 1 = 2)
下表为求得的David的修正评分:

则David对Kacey Musgraves的预测评分为:

转换为5星评价体系为:

最终的预测结果为4.506分。
Slope One算法
还有一种比较流行的基于物品的协同过滤算法,名为Slope One,它的最大的优势是简单,因此易于实现。
我们用一个简单的例子来了解这个算法。假设Amy给PSY打了3分,Whitney Houston打了4份;Ben给PSY打了4分。我们要预测Ben会给Whitney Houston打几分。
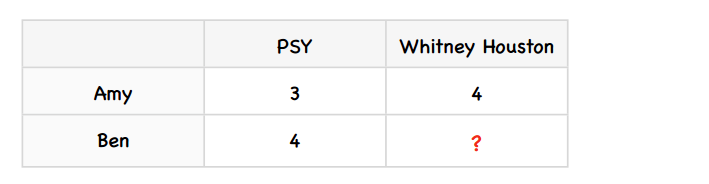
第一步:计算差值
我们先为上述例子增加一些数据:
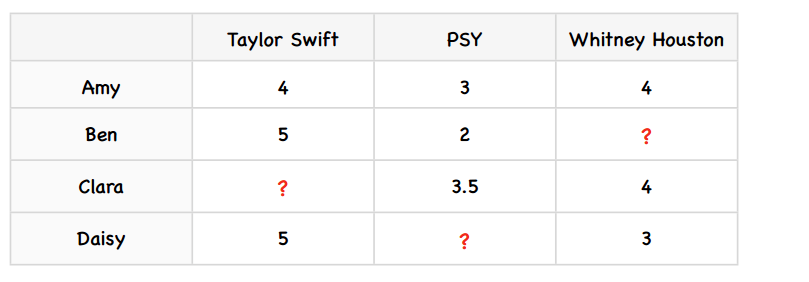
计算物品之间差异的公式是:

其中,card(S)表示S中有多少个元素;X表示所有评分值的集合;)) 表示同时评价过物品j和i的用户数。
表示同时评价过物品j和i的用户数。
我们来考察PSY和Taylor Swift之间的差值,因为只有两个用户(Amy和Ben)同时对PSY和Taylor Swift打过分。
$$ dev_{swift, psy} = (4-3)/2 + (5-2)/2 = 2 $$
所以PSY和Taylor Swift的差异为2。反过来,Taylor Swift和PSY的差异:
$$ dev_{psy, swift} = (3-4)/2 + (2-5)/2 = -2 $$
其他物品之间的差异
0 | Taylor Swift | PSY | Whitney Houston
-|-
Taylor Swift | 0 | 2 | 1
PSY | -2 | 0 | -0.75
Whitney Houston | -1 | 0.75 | 0
第二步:使用加权的Slope One算法进行预测
公式为:
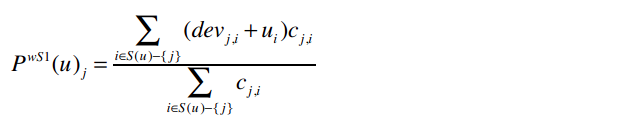
其中:
))
_{j}) 表示我们将预测用户u对物品i的评分。比如
表示我们将预测用户u对物品i的评分。比如_{Whitney Houston}) 表示Ben对Whitney Houston的预测评分。
表示Ben对Whitney Houston的预测评分。
-\{j\}} }) 表示遍历Ben评价过的所有歌手,除了Whitney Houston之外。
表示遍历Ben评价过的所有歌手,除了Whitney Houston之外。
整个分子的意思是:对于Ben评价过的所有歌手(Whitney Houston除外),找出Whitney Houston和这些歌手之间的差值,并将差值加上Ben对这个歌手的评分。同时,我们要将这个结果乘以同时评价过两位歌手的用户数。
Slope One的Python实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
users2 = {"Amy": {"Taylor Swift": 4, "PSY": 3, "Whitney Houston": 4},
"Ben": {"Taylor Swift": 5, "PSY": 2},
"Clara": {"PSY": 3.5, "Whitney Houston": 4},
"Daisy": {"Taylor Swift": 5, "Whitney Houston": 3}}
class Recommender():
def __init__(self, data, k=1, metric='pearson', n=5):
self.data = data
# 以下变量将用于Slope One算法
self.frequencies = {}
self.deviations = {}
def computeDeviations(self):
"""
计算物品之间的差异
:return:
"""
# 获取每位用户的评分数据
for ratings in self.data.values():
# 对于该用户的每个评分项(歌手、分数)
for (item, rating) in ratings.items():
self.frequencies.setdefault(item, {})
self.deviations.setdefault(item, {})
# 再次遍历该用户的每个评分项
for (item2, rating2) in ratings.items():
if item != item2:
# 将评分的差异保存到变量中
self.frequencies[item].setdefault(item2, 0)
self.deviations[item].setdefault(item2, 0.0)
self.frequencies[item][item2] += 1
self.deviations[item][item2] += rating - rating2
for (item, ratings) in self.deviations.items():
for item2 in ratings:
ratings[item2] /= self.frequencies[item][item2]
def slopeOneRecommendations(self, userRatings):
"""
加权的Slope One算法
:param userRatings:
:return:
"""
recommendations = {}
frequencies = {}
# 遍历目标用户的评分项(歌手、分数)
for (userItem, userRating) in userRatings.items():
# 对目标用户未评价的歌手进行计算
for (diffItem, diffRatings) in self.deviations.items():
if diffItem not in userRatings and userItem in self.deviations[diffItem]:
freq = self.frequencies[diffItem][userItem]
recommendations.setdefault(diffItem, 0.0)
frequencies.setdefault(diffItem, 0)
# 分子
recommendations[diffItem] += (diffRatings[userItem] + userRating) * freq
# 分母
frequencies[diffItem] += freq
recommendations = [(k, v / frequencies[k]) for (k, v) in recommendations.items()]
# 排序并返回
recommendations.sort(key=lambda artistTuple: artistTuple[1], reverse=True)
return recommendations
>>> r = Recommender()
>>> r.computeDeviations()
>>> r.deviations
{'PSY': {'Taylor Swift': -2.0, 'Whitney Houston': -0.75}, 'Taylor Swift': {'PSY': 2.0, 'Whitney Houston': 1.0}, 'Whitney Houston': {'PSY': 0.75, 'Taylor Swift': -1.0}}
>> > r.slopeOneRecommendations(users2['Ben'])
[('Whitney Houston', 3.375)]
|
参考
1,《集体智慧编程》
2, https://github.com/egrcc/guidetodatamining/blob/master/chapter-3.md


表示物品i和N的相似度,
表示用户u对物品N的评分。






表示同时评价过物品j和i的用户数。
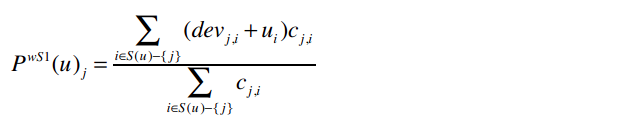
表示我们将预测用户u对物品i的评分。比如
表示Ben对Whitney Houston的预测评分。
表示遍历Ben评价过的所有歌手,除了Whitney Houston之外。